Az éjszakai égbolton városi fények mellett általában csak néhány csillagot tudunk megpillantani. Ahol kevésbé zavarnak a mesterséges fények, több százat is észrevehetünk, tökéletes körülmények között pedig elvileg 3-4000 csillagot is látni. Ez a szám azonban eltörpül a Galaxisunkban található kétszázmilliárd csillaghoz képest. Még ha be is kell látnunk, hogy az irdatlan távolságok, valamint a por- és gázfelhők miatt legtöbb hullámhosszon korlátozottak a lehetőségeink, akkor is akár több milliárd csillagról nyerhetünk pontos adatokat. Ez pedig már nem csak elmélet: a Gaia űrszonda több évnyi elképesztően precíz méréseinek köszönhetően minden eddiginél több csillagról vannak pontos információink. Pozíció, távolság, sebesség, fényesség, típus… mindez egyetlen óriási adatbázisban.
 Az Európai Űrügynökség (ESA) szondája, a Gaia. (Forrás: ESA)
Az Európai Űrügynökség (ESA) szondája, a Gaia. (Forrás: ESA)
Megmérni egy asztrofizikai objektum fenti adatait nem is olyan egyszerű. A pozíció mérése jobbára mérnöki kihívás, viszont így csak egy kétdimenziós koordinátarendszerben adhatjuk meg a csillag helyét – márpedig ez önmagában kevés. Akárcsak a csillagok, amiket az égbolton közel látunk egymáshoz (pl. egyazon csillagképben), valójában óriási távolságokra lehetnek egymástól, mivel a harmadik térbeli koordinátájukban (ebben az esetben a megfigyelőtől mért távolságuk) jelentős eltérés lehet.
 A Gaia űrszonda, itt még összeszerelés alatt. (Forrás: Astrium)
A Gaia űrszonda, itt még összeszerelés alatt. (Forrás: Astrium)
Itt jön képbe a Gaiai egyik nagy fegyverténye, az elképesztően precíz parallaxis-mérés. Ennek lényege egy egyszerű kísérlettel szemléltethető. Tartsuk magunk elé feltartott mutatóujjunkat, célozzuk meg vele egy falon lévő tárgyat, pl. képet. Csukjuk be a jobb szemünket és vizsgáljuk meg hol látjuk az ujjunkat a képhez képest pusztán a bal szemünkkel. Majd váltsunk a jobb szemünkre – ekkor a falon lévő tárgyhoz képet az ujjunk látszólag balra ugrott. Tehát ha a megfigyelő ugyanabból a távolságból, de eltérő irányból szemlél egy objektumot (a mutatóujjunkat) a háttérhez (a falon lévő képhez) képest más pozícióban fogja látni. Ráadásul a két pozíció közti látszólagos eltérésből, illetve a megfigyelési helyek távolságából (ez a bázisvonal, az előbbi példában a szemeink közti távolság) ki lehet számítani a megfigyelt objektum távolságát – ezzel pedig el is jutottunk a harmadik térbeli koordinátához. A Gaia esetében a parallaxis-mérés bázisvonalát az L2 (Lagrange)-pont körüli pályájának két legtávolabbi pontja adja (ami nagyjából 700.000 km), a mérendő objektum nyilvánvalóan a csillag, a ’’háttér’’ pedig maga a koordináta-rendszer.
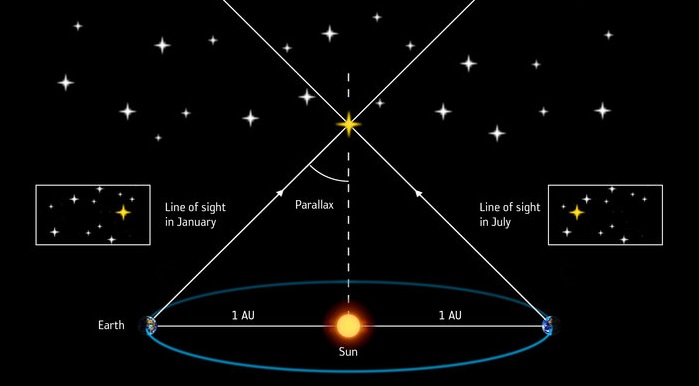 A Földről történő parallaxis-mérés vázlata. (Forrás: ESA)
A Földről történő parallaxis-mérés vázlata. (Forrás: ESA)
A Gaia misszió 2014 szeptemberében érkezett meg az L2-höz és kezdte meg a méréseket, amelyeket a tervek szerint 2019 végéig fog folytatni (a katalógus csak akkorra válik teljessé, azonban már a mostani adatok nyilvánosságra hozatala is óriási jelentőségű). Ez idő alatt a mérendő objektumok átlagosan hetvenszer kerülnek az űrteleszkóp látómezőjébe – ezzel a cél egyfelől a pontosság növelése (hiszen mérési hiba mindig van, ez több méréssel csökkenthető), másrészt a koordináták időbeli változásának, vagyis a csillagok sajátmozgásának kimérése. Ez a sebességvektor önmagában azonban megint csak két dimenziós, a harmadik, ún. radiális sebességkomponenshez (vagyis, hogy hozzánk képest közeledik vagy távolodik-e az objektum) újabb mérés-típusra van szükség.
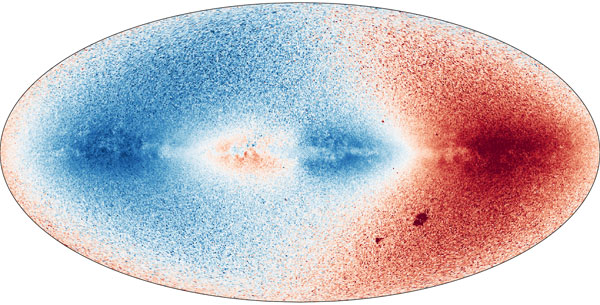 A Tejútrendszer csillagainak radiális sebesség-térképe, amelyen jól kivehető a Galaxis rotációja. A jobb alsó negyedben jól kivehető a Kis- és Nagy Magellán-felhő vörös foltja. (Forrás: SPAC/ESA)
A Tejútrendszer csillagainak radiális sebesség-térképe, amelyen jól kivehető a Galaxis rotációja. A jobb alsó negyedben jól kivehető a Kis- és Nagy Magellán-felhő vörös foltja. (Forrás: SPAC/ESA)
A Gaiai ugyanis spektrumokat (magyar szóval színképeket) is felvesz a csillagokról, amelyek gyakorlatilag a forrás által kibocsájtott fény hullámhossz szerinti eloszlásai. Ezekben fellelhetőek a csillag külső légkörét alkotó gázok által keltett spektrumvonalak, amelyek mintegy vonalkódszerűen az egyes kémiai elemekre jellemzőek. A Gaia esetében azonban nem a kémiai analízis az elsődleges cél, hanem a spektrumvonalak Doppler-effektus által okozott elmozdulása. Ezt középiskolában is tanított jelenséget (emlékezz, a közeledő és távolodó sziréna hangja más frekvenciájú/hullámhosszú) a csillag sajátmozgásából fakadó közeledése vagy távolodása okozza: előbbi esetben a spektrálvonalak a rövidebb-, utóbbi esetben pedig a hosszabb hullámhosszak irányában tolódnak el. Az eltolódás mértékéből pedig közvetlenül kiszámolható a radiális sebesség (hasonló módon keresnek exobolygókat csillagok körül).
 Mozgó fényforrások színképeinek Doppler-eltolódása.
Mozgó fényforrások színképeinek Doppler-eltolódása.
A pozíció és a sebesség pedig még nem minden. A Gaiai-t ugyan nem képalkotásra tervezték, viszont képes az egyedi objektumok fényességét (illetve annak időbeli változását) mérni, ráadásul a kék és vörös színtartományban is. A távolságkoordináta ismeretében így kiszámítható a csillagok valódi fényessége (más néven luminozitása), amelyet nem befolyásol az, hogy milyen messze vannak a Földtől (hiszen egy fényforrás látszó fényessége a távolsággal négyzetesen csökken). A spektrumok a luminozitásokkal kiegészülve alkalmasak arra, hogy segítségükkel kiszámíthassuk a csillagok ún. légköri paramétereit (hőmérséklet, fémtartalom, nehézségi gyorsulás); míg a fénygörbékkel együtt a változócsillagok típusa is megállapítható. És akkor még nem is beszéltünk a járulékos felfedezésekről, mint a mérések közben a látómezőbe tévedő naprendszerbeli aszteroidák, illetve a távoli galaxisokban fellelhető kvazárok detektálásáról.
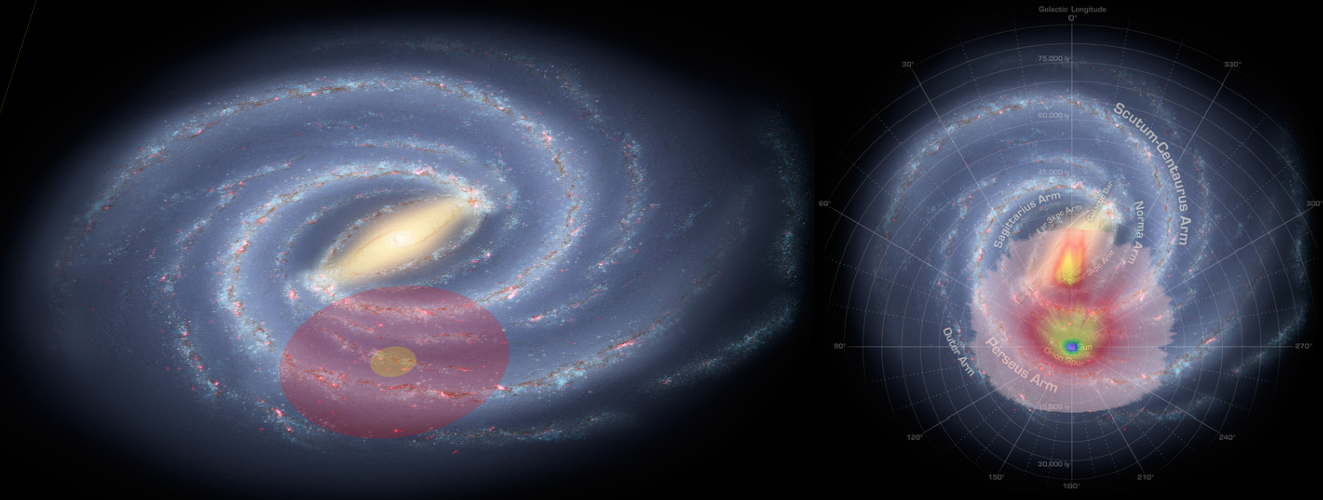 Balra a Gaia (pirossal) és az előző generációs asztrometriai űrszonda, a Hipparcos (sárga) által vizsgált csillagok hozzátevőleges pozíciója a Galaxisban. Jobbra a Gaia által kimért csillagok száműrűsége (a legtöbb csillagot tartalmazó régió pirossal jelölve). (Forrás: Robert Hurt (NASA-JPL/Caltech)/X. Luri & the DPAC-CU2)
Balra a Gaia (pirossal) és az előző generációs asztrometriai űrszonda, a Hipparcos (sárga) által vizsgált csillagok hozzátevőleges pozíciója a Galaxisban. Jobbra a Gaia által kimért csillagok száműrűsége (a legtöbb csillagot tartalmazó régió pirossal jelölve). (Forrás: Robert Hurt (NASA-JPL/Caltech)/X. Luri & the DPAC-CU2)
A Gaia legnagyobb fegyverténye azonban nem az adatok sokszínűségében rejlik, hanem a mérések precizitásában és az elképesztő mennyiségű objektumban. Előbbire jó példa a pozíciómérés 7-20 mikroívmásodperes bizonytalansága – ez a szögméret gyakorlatilag megfelel egy hajszál vastagságának 1000 km-ről vizsgálva!
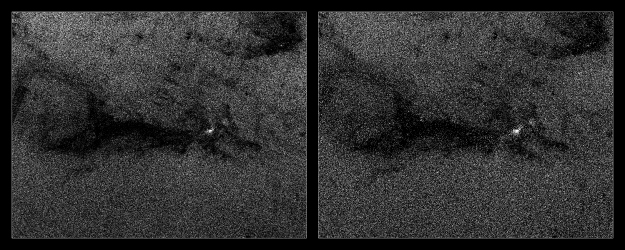 A ‘Róka’ névre hallgató sötét nebula az Orion Molekulafelhőben, ahogy a Gaia látja. Mivel az űrszondát nem képalkotásra tervezték, ezeket a ”felvételeket” pixelenként kellett összrakni a csillagok pozícióiból (balra), majd hozzátársítani a fényességüket (jobbra). Ahol nem látszik csillag, ott van a felhő. A róka szeme az Orion nyílthalmaz (M42). (Forrás: Gaia DPAC/André Moitinho, Márcia Barros, Carlos Barata)
A ‘Róka’ névre hallgató sötét nebula az Orion Molekulafelhőben, ahogy a Gaia látja. Mivel az űrszondát nem képalkotásra tervezték, ezeket a ”felvételeket” pixelenként kellett összrakni a csillagok pozícióiból (balra), majd hozzátársítani a fényességüket (jobbra). Ahol nem látszik csillag, ott van a felhő. A róka szeme az Orion nyílthalmaz (M42). (Forrás: Gaia DPAC/André Moitinho, Márcia Barros, Carlos Barata)
Ami pedig a nagy számokat illeti: már most 1,7 milliárd (!!!) csillagnak sikerült megmérni a pozícióját és fényességét. Ez az elképesztő szám ugyan kevesebb, mint 1%-a a Tejútrendszer össz-csillagszámának (ne feledjük, a távolságok, valamint a csillagközi por- és gáz-felhők miatt nem is látjuk a Galaxisunk nagy részét), viszont nagyságrenddel több adat, mint amivel eddig rendelkeztünk. Nagyobb hányaduknak, mintegy 1,3 milliárd csillagnak immáron a távolságát is ismerjük, így végre valódi 3D-s térképet alkothatunk a Naprendszer (néhány ezer fényév sugarú) környezetéről.
 A Gaia-katalógus állapota a mostani adatdömping után: adatok csak nem 1,7 milliárd csillagról, több tízezer kvazárról és tizennégyezer aszteroidáról. (Forrás: ESA)
A Gaia-katalógus állapota a mostani adatdömping után: adatok csak nem 1,7 milliárd csillagról, több tízezer kvazárról és tizennégyezer aszteroidáról. (Forrás: ESA)
Végezetül álljon itt egy csoportkép az 1,7 milliárd csillagról. Az alábbi kép első ránézésre semmiben sem különbözik az űrtávcsövek (vagy az asztrofotósok) több felvételből összeollózott Tejútrendszer-fotóitól – csakhogy a Gaia űrszonda nem tud képet alkotni. Ehelyett az űrtávcső adatait feldolgozó csillagászok a kimért koordináták szerint helyezték el az 1,7 milliárd fénypontot, fényességüknek és színüknek megfelelően, megalkotva ezzel a legnagyobb csillagtérképet. És mindez még csak a kezdet; a teljes katalógusra egészen 2022-ig kell várni.
 A Gaia által mért csillagok fénye és színe a pozíciójuknak megfelelően: ahogy mi látjuk a Galaxist. (Forrás: Gaia DPAC / A. Moitinho, A. F. Silva, M. Barros, C. Barata (Univ. of Lisbon, Portugal) / H. Savietto (Fork Research))
A Gaia által mért csillagok fénye és színe a pozíciójuknak megfelelően: ahogy mi látjuk a Galaxist. (Forrás: Gaia DPAC / A. Moitinho, A. F. Silva, M. Barros, C. Barata (Univ. of Lisbon, Portugal) / H. Savietto (Fork Research))
Ha tetszett a bejegyzés, látogass el a Csillagvizsgáló blog Facebook oldalára is, ahol napi rendszerességgel találhatsz látványos felvételeket, friss tudományos eredményeket és egyéb aktualitásokat.
