Már szabad szemmel is pislákoló csillagok ezreit pillanthatjuk meg az égen, de távcsőbe nézve ez a csillagfalu sztelláris megapoliszként tárul elénk, és ilyenkor felmerül a kérdés: “No de milyen messze látunk el ezzel a távcsővel?”. Az égitestek térbeli elhelyezkedését az égbolton nem tudjuk érzékelni. nem tudjuk az égitestek térbeli elhelyezkedését érzékelni. Pusztán az éggömb felszínén elfoglalt pozíciójukat, vagyis az irányukat, valamint a fényességüket tudjuk megmondani. De akkor miként határozzák meg a csillagászok a világűr változatos objektumainak távolságát? Hogyan derül ki, hogy galaktikus bolháról, vagy kozmikus elefántról beszélünk? És miként lehetséges a megállapított távolságok és méretek igazolása, ha mindezen objektumok elérhetetlenek a számunkra? Ötrészes sorozatunkban lépésről lépésre vesszük végig a csillagászati távolságmérés létráját – kezdésként pedig tisztázzuk az alapfogalmakat!
A déli féltekéről látszó égbolt, ami tele van a nagy hajós felfedezőutakat megörökítő csillagképekkel, melyek közül számos az égitestek pozíciójának mérésére használt eszközt jelenít meg, úgy mint Körző, Szögmérő, Oktáns, Szextáns. (Forrás: Stellarium)
A távolságmérési módszereknek alapvetően két típusát különböztetjük meg, a geometriai és a (tág értelemben vett) fotometriai eljárásokat. Előbbi esetében egy objektum valamilyen független forrásból ismert elmozdulását és annak az égen való vetületét hasonlítjuk össze, amelyből következtetni lehet a megfigyelt objektum távolságára. Az elmozdulás lehet valós vagy a megfigyelő mozgása miatt akár látszólagos is, a lényeg, hogy a kiváltó hatás mértéke ismert legyen. Ennek birtokában mindössze az adott objektum kétdimenziós égbolton megfigyelt elmozdulásának szögtávolságát, vagyis az előtte és utána felvett pozícióinak a megfigyelővel bezárt szögét kell kimérni. A szögeket a matematikaórán megismert fokokkal vagy az ívszámításból eredeztetett radiánnal jellemezzük:
- 360 fok = 2π (‘pí’) radián – teljes “körbenézés”, példa: Feszty-körkép;
- 90 fok – derékszög, példa: a horizonttól a fejünk feletti ún. zenit pontig tartó szög (ha eltekintenénk a Föld görbületétől);
- 1 fok – kb. 53 cm-ről nézve az egyforintos érme, az égbolton a Nap vagy a telihold korongjának a duplája (Előbbibe megfelelő szemvédő szűrő nélkül semmiképp se nézzünk!);
- 1 ívperc (az 1 fok 60-ad része) – az egyforintos érme bő 30 méterről szemlélve, az emberi szem felbontóképességének határa;
- 1 ívmásodperc (az 1 ívperc 60-ad része) – az ötforintos érme 4 km-ről vizsgálva; légkörünk tulajdonságai miatt a Föld felszínéről használt, tisztán optikai eszközök elméleti felbontóképességének határa;
- 1 mas (milliívmásodperc, az ívmásodperc ezredrésze) – a Holdon maradt (2,3 méter széles, 3,1 méter hosszú) holdautók látszó mérete a Föld távolságából (380 000 km messziről);
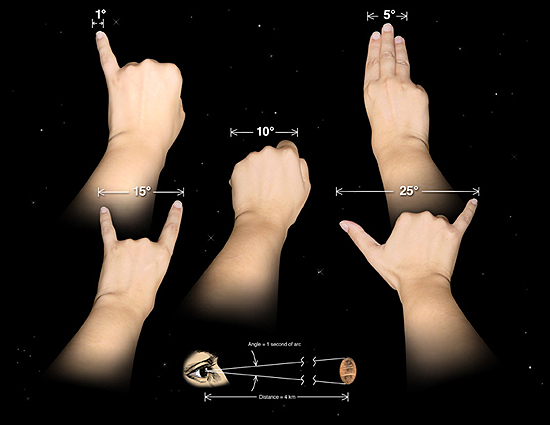Az égitestek égi pozícióinak szögtávolságához használt ököl-szabályok. Kinyújtott karral kézfejünk ábrán látható tartásaiban nagyjából az ott feltüntetett szögtávolságokat érik át, például kisujjunkkal le tudnánk takarni két Holdat is egymás mellett. Természetesen ezek csak becslésekre alkalmasak, hiszen az emberek testfelépítése egészen változatos, de nagyságrendileg (átlagos testfelépítés mellett) megállják helyüket mindenkinél.
Utóbbi elképesztően alacsony szögtávolságok manapság már (megfelelő felbontás esetén) kimérhetőek. A megfigyelt szög (egy adott kiváltó hatás esetén) pedig annál kisebb, minél távolabb van az objektum – vagyis a technológia fejlődésével egyre messzebbre tudjuk kiterjeszteni a geometriai távolságmérési módszerek hatékonyságát.
A csillagászati távolságmérési módszerek zöme az objektumok fényességén alapul. Elsőre azt gondolhatná az ember, hogy a fényesebb csillagok a közelebbiek, a halványak pedig a távolabbiak, ehhez azonban azt kellene feltételeznünk, hogy a csillagok mind ugyanolyan fényesek (amiről már csak azok különböző színét látva is sejthetjük, hogy nem igaz). A fotometrián, azaz fényességmérésen alapuló módszerek során az égitestek megfigyelt és valamilyen megfelelően alátámasztott modellből származtatott elméleti fényességét vetjük össze, és vonjuk le belőle a távolságra vonatkozó következtetéseinket.
A fotometriai eljárások megértéséhez elsőként azt kell tisztáznunk, hogy miben mérjük a fényességet? Az égitestek fényességének alapegységeként a magnitúdót szokás használni, ami pár fokkal komplikáltabb mértékegység, mint a hétköznapi életben alkalmazottak. Még az ókori görög csillagász, Hipparkhosz vezette be a fényrend fogalmát, amikor 6 különböző kategóriába sorolta a csillagokat, melyek közül a legfényesebbek tartoztak az 1-es és a leghalványabbak a 6-os fényrendbe.
Egy magnitúdó-különbség 2,5-szeres fényesség-különbséget jelent, vagyis a Deneb csillag (m ~ 1 magnitúdó) kb. százszor fényesebb tőlünk szemlélve, mint az Uránusz bolygó (m ~ 6 magnitúdó).
A dolog a XIX. században kezdett bonyolódni, amikor Ernst Heinrich Weber (1795–1878) és Gustav Theodor Fechner (1801–1887) fiziológiai kutatásai nyomán kiderült, hogy az emberi érzet és a kiváltó inger intenzitása nem lineárisan függ egymástól (a 2x-3x-4x nagyobb érzet kiváltásához nem 2x-3x-4x nagyobb ingerre van szükség). Vagyis ha a fent meghatározott fényrendeket szeretnénk használni (valamilyen perverz indíttatásból és/vagy hagyománytiszteletből), akkor két különböző fényességű objektum fényességértékének különbségét az intenzitások arányának logaritmikus összefüggése adja meg. Ráadásul a magnitúdóskála az eredeti definíció szerint még fordított is, hiszen az egyre halványabb csillagokhoz rendelünk egyre nagyobb számértékeket. Szóval kész őrület… de hozzá lehet szokni.
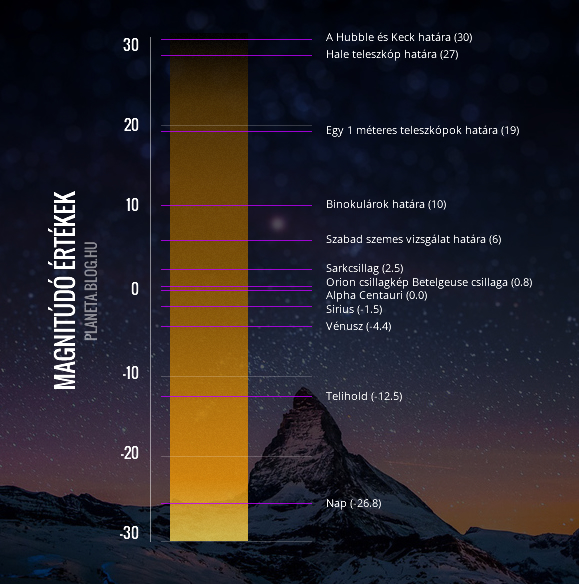A legismertebb égitestek és a optikai eszközök látszó fényességei, (felső, azaz leghalványabb) fényességhatárai (Forrás: Planéta blog)
Ha már otthonosan mozgunk a magnitúdóskálán, akkor viszont könnyen lefordíthatjuk távolságinformációra. Válasszunk egy referenciatávolságot (a 10 parszek a szokásosan használatos), és az abból a távolságból érzékelhető fényességet hívjuk abszolút fényességnek. Ennek és a megfigyelt fényességnek a különbségét pedig nevezhetjük távolságmodulusnak, hiszen a különböző távolságokba eljutó intenzitások aránya egyenesen következik a távolságok arányából. Az intenzitás ugyanis a távolsággal négyzetesen csökken, ahogy a gömbfelület – amelyen az adott fénymennyiség tovaterjedve eloszlik – a forrástól mért távolsággal (négyzetesen) növekszik. Vagyis, ha megmérjük egy égitest (tőlünk) látszó fényességét, és valamilyen független eljárásból ismerjük az abszolút fényességét, akkor meg tudjuk becsülni a kérdéses objektum távolságát. Persze semmi sem tökéletes, így itt is figyelembe kell venni olyan zavaró tényezőket, mint a csillagközi anyag fényelnyelése, ami miatt valamivel kevesebb fény jut el hozzánk, mintha csak egyszerűen vákuumban terjedt volna tova a fény.
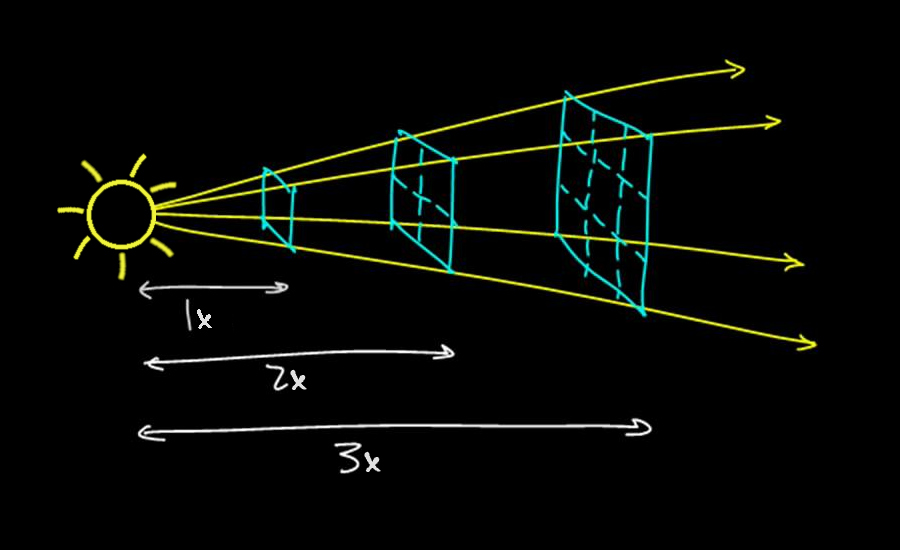
A forrástól mért távolsággal együtt a felület is növekszik, amin eloszlik a kisugárzott fénymennyiség, méghozzá négyzetesen.
(Forrás: Derek Owens)
Természetesen itt érdemes kicsit elrugaszkodni a hétköznapi életben használatos távolságegységektől, és nagyobb “méterrudakat” használni, amikből nem kell olyan sok, hogy átérje a kérdéses távolságot.
Csillagászati egység (röviden: CSE. vagy angol rövidítésből: AU) – 149 597 870,7 kilométer
Az első alapvető csillagászati távolságegység a Föld–Hold-rendszer tömegközéppontja által kijelölt Nap körüli pálya fél nagytengelye. Összehasonlításként ez a Föld egyenlítői átmérőjének bő tízezerszerese! Mivel a távolságmérés hibája szinte minden esetben bőven nagyobb a kerekítési hibánál, ezért a legtöbbször nemes egyszerűséggel a 150 000 000 km (százötven millió kilométer) értéket szokás használni. (A szemfüles olvasó észreveheti, hogy a definíció megalkotásakor elhagytuk ennek az alapvetően mért értéknek a hibáját, mentségünkre legyen mondva, a Nemzetközi Csillagászati Unió [IAU] döntése alapján).
Fényév (angol rövidítésből: ly) – 9 460 730 472 580,8 kilométer = ~ 63 241 CSE
Mivel jóval nagyobb távolságokat is szeretnénk könnyen kezelni a számolások során, érdemes új távolságegységet alkotnunk. A fényév nevéből eredően könnyen megjegyezhető definícióval rendelkezik: a távolság, amelyet a fény egy év alatt megtesz… na akkor pontosítsunk! A fény a különböző közegekben különböző sebességgel terjed, viszont vákuumban való terjedési sebessége a relativitáselmélet értelmében felső határsebesség is, aminél gyorsabban semmilyen információ vagy kölcsönhatás nem terjedhet. Válasszuk hát ezt (röviden írva) fénysebességnek, amely 299 792,458 km/s (kilométer másodpercenként)! De az év sem pontosan 365 (vagy 366) napos annak fizikai értelmében, hiszen a Föld Nap körüli pályáját nem pontosan ennyi idő alatt járja be. Itt is az IAU döntésére érdemes hagyatkoznunk, amely évként a 365,25 (egyesével 86 400 SI másodperces) napból álló julián év mellett döntött (ami 31 557 600 másodperccel egyenlő). Szemléletesen a Nap tőlünk vett (nagyjából átlagos) távolsága csak 1 az ebbe a távolságba beleférő 63 241 csillagászati egységből, illetve a legközelebbi csillag fényének is 4,2 évet kell utaznia, mire elér hozzánk. Ebből is jól látszik, hogy amint kilépünk Naprendszerünkből, a CSE. méterrúdját a legtöbb esetben célszerű hátrahagyni.
Parszek (röviden: pc) – 30 856 775 814 913, 673 kilométer = 3,26 fényév = ~ 206 265 CSE
Egy hasonló nagyságrendű, de egészen más alapokon nyugvó alap távolságegység a parszek. Valójában a geometriai távolságmérés alapegységéről beszélünk, ugyanis ez az a távolság, amelyből a Nap–Föld (átlagos) távolság(hoz közel eső 1 CSE) egy ívmásodperc (az egy fok 3 600-ad része (azaz a teljes kör 1 296 000-ed része)) alatt látszik. Ezt talán úgy lehet a legjobban elképzelni, hogy egy 5 forintos pénzérme két átellenes széle látszik ugyanekkora szög alatt néhány kilométer távolból. Ez a szögméret egyben nagyjából a legkisebb szögméret is, amelyet a földi légkör alól az égre nézve meg tudunk különböztetni – fel tudunk bontani – valamilyen optikai eszközzel, köszönhetően a légkör állandó mozgásának és fénytörésének.
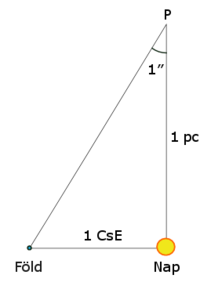
A csillagászati egység és a parszek közti geometriai összefüggés (az ábrán a távolságok és szögek aránya a valóságtól eltér, mivel ilyen kis szög és ilyen nagy távolságarány a kijelzők adott méretei mellett nem ábrázolható arányosan). (Forrás: nkp.hu)
A következő részekben ezekre az ismeretekre támaszkodva a legkisebb távolságoktól az egyre nagyobb távolságokba merészkedve fedezzük fel a különböző egymásra épülő módszereket. A mindennek az alapjául szolgáló geometriai módszerből kiindulva haladunk majd végig az egyedi objektumok fotometriai módszerein és a galaxisok távolságmérésén át egészen a kozmológiai távolságmérésekig, egyesével lépkedve végig a kozmikus távolságlétra lépcsőfokait.
A távolságlétra (avagy méterrúd) egymásra épülő módszerei révén jutunk el a kozmikus szomszédságunktól a Világegyetem méreteinek meghatározásáig. (Kép: Grzegorz Pietrzyński)
Ha tetszett a bejegyzés, látogass el a Csillagvizsgáló Facebook oldalára is, ahol napi rendszerességgel találhatsz csillagászati és űrkutatási híreket, látványos felvételeket és egyéb aktualitásokat – tudományról és science fiction-ről egyaránt.